Na deze concrete toepassing en het grote onderzoek werken we toe naar het formele rekenen rondom procenten.

Alles wordt duurder en de broeken in deze zaak zijn in twee jaar gemiddeld 25% duurder geworden.

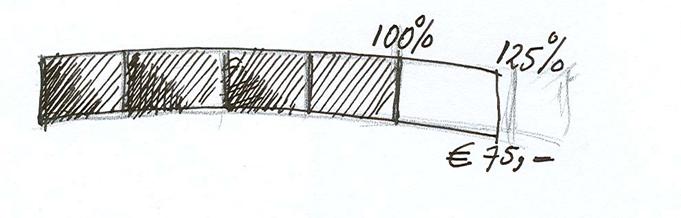
Karel koopt zijn favoriete broek en moet daar 75€ voor betalen.
Wat was de prijs van de broek 2 jaar geleden?
Er is 25% bijgekomen, wat betekent dat nu 125% een bedrag van 75 € oplevert.
Wat kostte die broek toen?

Nu 5 delen van 25%, samen 75€. 1/5 deel is 15€. 4/5 deel (100%) is dus 4x15€ is 60€.
Op deze manier zijn er allerlei opdrachten te bedenken of te vinden die m.b.v. breuken opgelost kunnen worden.